Introduction

Given an N*N matrix, find the maximum submatrix. If all the integers are negative, the maximum sum will be 0.This problem can be seen as the expansion of the Maximum Subsequence Sum problem in the textbook.

Algorithm Specification

We have three solutions to this problem.

$O(N^6)$
$O(N^4)$
$O(N^3)$

Algorithm1
It’s the simplest solution, we just need to enumerate every submatrix and calculate the sum of every submatrix.
Fuction Solver

for ix in 1...n
    for jx in 1...ix
        for iy in 1...n
            for jy in 1...iy
                if Sum(jx, jy, ix, iy) > Ans
                    Ans = Sum(jx, jy, ix, iy);

Fuction Sum

1
2
3

for i in jx...ix
    for j in jy...iy
        Ans += a[i][j];

Algorithm2
We can easily find that we can use a 2-dimension array to represent the Sum of a submatrix.
We define $Sum[x][y] = \sum{i=1}^{x}\sum{j=1}^{y}a[i][j]$
The following pseudo-code can help you understand how to calculate it.

for i in 1...n
    for j in 1...n
        Sum[i][j] = Sum[i][j - 1] + a[i][j];
for i in 2...n
    for j in 1...n
        Sum[i][j] += Sum[i - 1][j];

Then we get a new Sum fuction.

1	return Sum[ix][iy] + Sum[jx - 1][jy - 1] - Sum[jx - 1][iy] - Sum[ix][jy - 1];

Then you can use Fuction Solver to calculate the answer.
Algorithm3
A submatrix have four borders, they are upper and lower ones of a row and left and right ones of the column. Then, we can enumerate the left and right borders of the column, relating it to the Maximum Subsequence Sum problem in the textbook.
We define $Sum[x][y] = \sum_{j=1}^{y}Sum[x][j]$
We can calculate it as follow.

1
2
3

for i in 1...n
    for j in 1...n
        Sum[i][j] = Sum[i][j - 1] + a[i][j];

Then if we choose column $i$ and $j$ $( i < j )$, we can let $val[x]= Sum[x][j] - Sum[x][i - 1]$ and use the solution for Subsequence Sum problem.

Testing Results

Case 1:

10
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 
-1 -1  1  1  1  1  1  1  1  1 
-1 -1  1  1  1  1  1  1  1  1 
-1 -1  1  1  1  1  1  1  1  1 
-1 -1  1  1  1  1  1  1  1  1 
-1 -1  1  1  1  1  1  1  1  1 
-1 -1  1  1  1  1  1  1  1  1 
-1 -1  1  1  1  1  1  1  1  1 
-1 -1  1  1  1  1  1  1  1  1 
-1 -1  1  1  1  1  1  1  1  1

This case is to test if algorithm2 can calculate the sum of a submatrix rightly.
The right answer is 72.
Program output is 72.
Status: Pass.

Case 2:

5 
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1

This case is to test if program can correctly handle all negtive numbers cases.
The right answer is 0.
Program output is 0.
Status: Pass.

Analysis and Comments

To enumerate a point, we need to enumerate x and y, x from $1$ to $n$ and y from $1$ to $n$. So, the time complexity of enumerating a point is $O(N^2)$.
Algorithm1
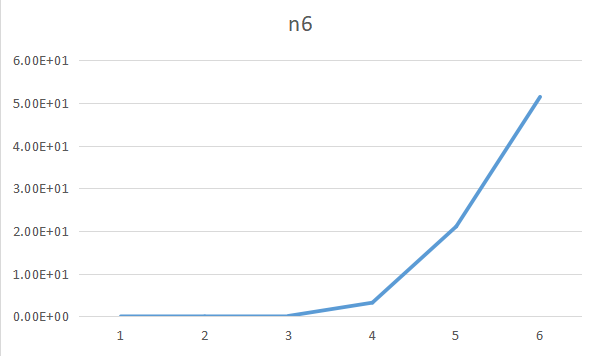
Time complexity:For algorithm1, we need to enumerate two points to determine a submatrix, and the time complexity is $O(N ^ 4)$.And the calculation of the sum of this submatrix is $O(N^2)$. Thus, this algorithm’s time complexity is $O(N^6)$.
Space complexity:In algorithm1, we use a $n\times n$ array $a[x][y]$ to store matrix. Thus, the space complexity of this algorithm is $O(N^2)$.
Algorithm2
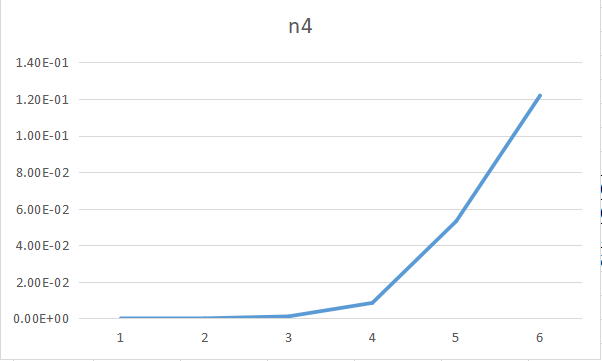
Time complexity:For algorithm2, we still need to enumerate two points, but we can know the sum of the submatrix in $O(1)$.The time complexity of enumerating two points is $O(N^4)$, and calculate $Sum$ array need $O(N^2)$. Finally, the time complexity of algorithm2 is $O(N^4)$.
Space complexity:For algorithm2, we use two $n \times n$ array $a[x][y], Sum[x][y]$. The space complexity of algorithm2 is $O(N^2)$.
Algorithm3
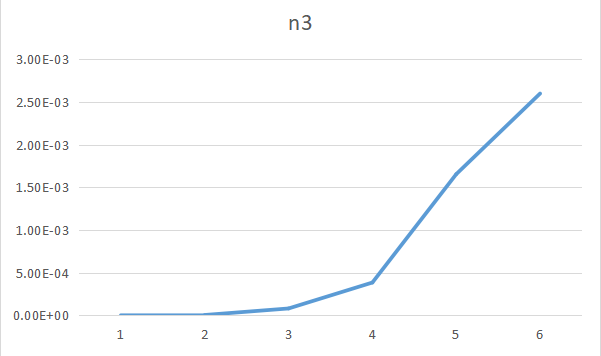
Time complexity:In algorithm3, we need to enumerate two columns, the complexity of that is $O(N^2)$, and for each of that, we will do an $O(n)$ algorithm to solve the Maximum Subsequence Sum problem. The time complexity of calculating $Sum[x][y]$ is $O(N^2)$.Thus the time complexity of algorithm3 is $O(N^3)$.
Space complexity:In algorithm3, we use two $n\times n$ array $Sum[x][y], a[x][y]$. Thus, the space complexity of algorithm3 is $O(N^2)$.
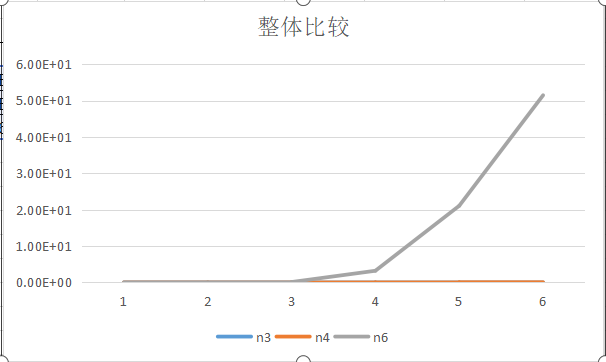
The comparasion of the three algorithms
The O(N^6) algorithm has to calculate the summary of every submatrix repeatedly. In comprison, the O(N^4) algorithm just calculates part of them,and then do some simple on work, which can save a lot of time.
The O(N^3) algorithm look to transfer the two-dimensional problem into an one-dimensional one, with the sum of each coloum put into a single cell of an one-dimensional array.Then we can find that all we have to do is to scan such an array for once, just like what we did to the problem in the textbook in the easiest way.This algorithm is apparently smarter than the ones before, as it avoid some unnecessary work.

PS:NULL represent the time needed is too long to record.

algorithm1
N	$5$	$10$	$30$	$50$	$80$	$100$
K	$100000$	$1000$	$1$	$1$	$1$	$1$
Ticks	$1480$	$462$	$114$	$3216$	$21076$	$51456$
Total Time	$1.48$	$0.462$	$0.114$	$3.216$	$21.076$	$51.456$
Duration	$1.48e-5$	$4.62e-4$	$0.114$	$3.216$	$21.076$	$51.456$

algorithm2
N	$5$	$10$	$30$	$50$	$80$	$100$
K	$10000$	$10000$	$1000$	$500$	$100$	$50$
Ticks	$17$	$211$	$1092$	$4235$	$5315$	$6095$
Total Time	$1.7e-2$	$2.11e-1$	$1.092$	$4.235$	$5.315$	$6.095$
Duration	$1.7e-6$	$2.11e-5$	$1.09e-3$	$8.47e-3$	$5.32e-2$	$0.1219$

algorithm3
N	$5$	$10$	$30$	$50$	$80$	$100$
K	$100000$	$100000$	$1000$	$200$	$200$	$100$
Ticks	$75$	$459$	$81$	$77$	$331$	$260$
Total Time	$7.5e-2$	$4.59e-1$	$8.1e-2$	$7.7e-2$	$3.31e-1$	$2.6e-1$
Duration	$7.5e-7$	$4.59e-6$	$8.10e-5$	$3.85e-4$	$1.66e-3$	$2.6e-3$

整体比较.png

Declaration
We hereby declare that all the work done in this project titled
“Finding the maximum submatrix” is of our independent effort as a group.